MATEMATICAS

Triangulo:

Resultados de búsqueda

Fragmento destacado de la Web

 Concepto: El triángulo es un polígono de tres lados. El triángulo está determinado por tres segmentos de recta que se denominan lados, o por tres puntos no alineados llamados vértices. Los lados de un triángulo se escriben en minúscula, con las mismas letras de los vértices opuestos.

propiedades: Un triángulo es un polígono de tres lados. En un triángulo, un mayor lado se opone a un mayor ángulo. El valor de un ángulo exterior de un triángulo es igual a la suma de los dos interiores no adyacentes. Un lado de un triángulo es más pequeño que la suma de los otros dos y mayor que su diferencia.

perímetro: a + b + c                                   

área: el área de un triángulo es igual a base por altura partido por 2 

Cuadrado

Concepto: Un cuadrado en geometría es un cuadrilátero regular, es decir, una figura plana de cuatro lados iguales y cuatro ángulos interiores rectos (90°), por lo que también es un rectángulo.

Propiedades: 

• Lados: el cuadrado tiene cuatro lados iguales y paralelos dos a dos.
• Ángulos: tiene cuatro ángulos iguales y rectos de 90º. Los ángulos interiores, como en
  
  todo cuadrilátero, suman 360º. 
• Diagonales: las diagonales son segmentos que unen los vértices opuestos. Tiene dos diagonales iguales y perpendiculares. Se cortan en el centro del cuadrado. Las diagonales son las bisectrices de los ángulos. También son ejes de simetría.
• Ejes de simetría: son líneas imaginarias que dividen el cuadrado en dos partes simétricas respecto a dicho eje. 

Area: L+L+L+L

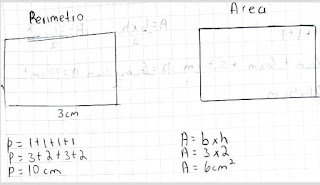
Perimetro: LxL

 

Rectangulo

Consepto: Es decir, el rectángulo es un cuadrilátero con dos pares de lados que miden igual y que, al mismo tiempo, son paralelos entre sí (no se cruzan, aunque se prolonguen).

Propiedades: tiene cuatro lados, siendo cada lado igual a su opuesto, es decir, dos a dos. Ángulos: sus cuatro ángulos son iguales y rectos de 90º . Los ángulos interiores, como en todo cuadrilátero, suman 360°.

Area: El área se calcula multiplicando la base por la altura

perimetro: Es la suma de los cuatro lados. 

Rombo:

Concepto: Un rombo es un paralelogramo que tiene los cuatro lados iguales y ángulos iguales dos a dos.

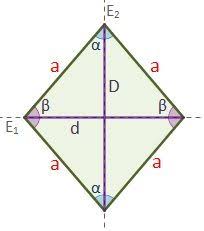
Propiedades: Sus 4 lados son iguales. Sus ángulos opuestos son iguales, es decir, los ángulos del rombo son iguales dos a dos. Sus diagonales son perpendiculares y se cortan en su punto medio. Sus dos diagonales son ejes de simetría del rombo.

Perimetro: El perímetro del rombo es igual a la suma de las longitudes de sus cuatro lados iguales.

Area: El perímetro del rombo es igual a la suma de las longitudes de sus cuatro lados iguales.

Trapecio: 

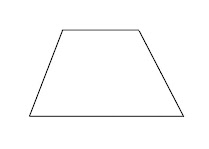
Concepto:  Es decir, el trapecio es un polígono con cuatro lados, cuatro ángulos interiores y dos diagonales. Su principal característica es que tiene solo dos lados paralelos, a diferencia de un paralelogramo donde ambos pares de lados opuestos son paralelos entre sí.

Propiedades:  

• La suma de los cuatro ángulos interiores equivale a cuatro rectos.
• Tiene dos diagonales en total, y desde un vértice se puede trazar solo una.
• Las diagonales se cortan en un punto interior del trapecio.
• El trapecio isósceles tiene sus lados no paralelos iguales, y sus ángulos bases iguales.
  
• Uno de los lados no paralelos del trapecio rectángulo, forma con las bases un ángulo de 900.

Propiedades: Un TRAPECIO RECTÁNGULO tiene dos ángulos rectos, uno agudo y otro obtuso. Puede tener dos lados iguales (isósceles) o todos distintos (escaleno). Pueden tener 1 o 2 ángulos obtusos, nunca cero, tres o cuatro. Si tiene un ángulo obtuso, entonces tendrá un ángulo agudo y dos rectos.

   Perímetro: El área del trapecio es igual a la suma de las bases por la altura, y dividido por dos.

  Área: El área del trapecio es igual a la suma de las bases por la altura, y dividido por dos.

Circulo: 

Propiedades: La distancia del centro del círculo a cualquier punto del círculo se llama radio. Cuando juntamos dos radios para formar un sólo segmento de recta cruzando el círculo, tenemos un diámetro. El diámetro de un círculo pasa por el centro del círculo y tiene sus puntos extremos en el círculo.

Concepto: Un círculo es una superficie plana limitada por una línea curva 

Área: El área del círculo es igual a pi por el radio al cuadrado.

Perimetro: El perímetro de un círculo es el doble del producto de π por el radio (r). También se puede calcular a partir del diámetro (D), siendo el producto de π y el diámetro. El perímetro del círculo es una circunferencia.

Pentágono: 

Concepto: El pentágono es una figura geométrica formada por cinco lados, además que tiene cinco vértices y cinco ángulos internos.

propiedades: 

• Los lados son iguales.
• Los ángulos internos son congruentes.
• Cada ángulo interno mide 108 grados.
• La suma de los ángulos internos de un pentágono regular es de 540° ó 3π radianes.
• 
  

Área: El perímetro es la suma de todos los lados. Si el polígono regular tiene n lados y la longitud del lado es l, el perímetro será igual a: P = n·l.

Perímetro: Su perímetro se calculará multiplicando su número de lados (cinco) por su longitud. Y se obtiene que el perímetro de este pentágono regular es de 10 cm

Hexágono: 

Concepto: En geometría plana elemental, un hexágono​​ o exágono es un polígono de seis lados y seis vértices.

Propiedades:

 Sus ángulos internos son congruentes midiendo 120° o rad.

Cada ángulo externo del hexágono regular mide 60° o. 

Está íntimamente relacionado con los triángulos equiláteros

Perímetro: El perímetro del hexágono es igual a la suma de las longitudes de sus seis lados.

Área: El área del hexágono regular es igual al perímetro por la apotema partido por dos.

Octágono: 

Concepto: Un octágono regular es un polígono de ocho lados y ocho ángulos iguales.

Propiedades:

Un octágono u octógono es un polígono de ocho lados y ocho vértices.

Un octágono regular es un polígono de ocho lados y ocho ángulos iguales.

Suma de ángulos interiores de un octágono = (8 − 2) · 180° = 1080°

El valor de un ángulo interior del octágono regular es 1080º : 8 = 135º

Perímetro: Su perímetro se calculará multiplicando su número de lados (cinco) por su longitud.

Área: esto significa que el área de un pentágono regular es igual al semiproducto del perímetro por el apotema.

Romboide:

Propiedades: 

tiene dos pares de lados opuestos, iguales y paralelos entre sí.

Cada par de ángulos contiguos son suplementarios.

Tiene dos ángulos agudos y dos obtusos.

Las bisectrices de los ángulos contiguos son perpendiculares entre sí.

Concepto: El romboide es un cuadrilátero, específicamente un paralelogramo, que tiene dos ángulos idénticos agudos (menores que 90º) y otro par de ángulos, también iguales, que son obtusos (mayores que 90º). Asimismo, dos de sus lados miden lo mismo, y los otros dos también comparten la misma longitud.

Área: El área del romboide es igual a base por altura.

Perímetro: El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados.

Utilidad del calculo de area y figuras planas: 

El perímetro y el área son magnitudes fundamentales en la determinación de un poligono o una figura geométrica; se utiliza para calcular la frontera de un objeto, tal como una valla. El área se utiliza cuando podemos obtener la superficie interior de un perímetro que se desea cubrir con algo, tal como césped o fertilizantes.

En el uso militar, el término perímetro define un área geográfica de importancia, como una instalación fisica o trabajo de la defensiva.

Si observamos a nuestro alrededor encontramos muchas figuras geométricas planas cuyos límites son segmentos. Por ejemplo las baldosas, las ventanas, obras de arte, etc.

El cálculo de áreas y perimetros desempeña un papel muy importante en nuestra sociedad. Constantemente debemos calcular áreas: para embaldosar un piso, empapelar una pared, comprar tela para realizar una prenda, lotear un terreno, etc.